
二叉树的深度
题目:
输入一个二叉树的根节点,求该树的深度。从根节点到叶子节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度包含的节点数为为树的深度,即二叉树节点的层数。
其实用一下图片能更好的理解LR模型和决策树模型算法的根本区别,我们可以思考一下一个决策问题:是否去相亲,一个女孩的母亲要给这个女海介绍对象。

大家都看得很明白了吧!LR模型是一股脑儿的把所有特征塞入学习,而决策树更像是编程语言中的if-else一样,去做条件判断,这就是根本性的区别。
决策树基于“树”结构进行决策的,这时我们就要面临两个问题 :
弄懂了这两个问题,那么这个模型就已经建立起来了,决策树的总体流程是“分而治之”的思想,一是自根至叶的递归过程,一是在每个中间节点寻找一个“划分”属性,相当于就是一个特征属性了。接下来我们来逐个解决以上两个问题。
在生活当中,我们都会碰到很多需要做出决策的地方,例如:吃饭地点、数码产品购买、旅游地区等,你会发现在这些选择当中都是依赖于大部分人做出的选择,也就是跟随大众的选择。其实在决策树当中也是一样的,当大部分的样本都是同一类的时候,那么就已经做出了决策。
我们可以把大众的选择抽象化,这就引入了一个概念就是纯度,想想也是如此,大众选择就意味着纯度越高。好,在深入一点,就涉及到一句话:信息熵越低,纯度越高。我相信大家或多或少都听说过“熵”这个概念,信息熵通俗来说就是用来度量包含的“信息量”,如果样本的属性都是一样的,就会让人觉得这包含的信息很单一,没有差异化,相反样本的属性都不一样,那么包含的信息量就很多了。
一到这里就头疼了,因为马上要引入信息熵的公式,其实也很简单:
Pk表示的是:当前样本集合D中第k类样本所占的比例为Pk。
信息增益
废话不多说直接上公式:

看不懂的先不管,简单一句话就是:划分前的信息熵–划分后的信息熵。表示的是向纯度方向迈出的“步长”。
好了,有了前面的知识,我们就可以开始“树”的生长了。
解释:在根节点处计算信息熵,然后根据属性依次划分并计算其节点的信息熵,用根节点信息熵–属性节点的信息熵=信息增益,根据信息增益进行降序排列,排在前面的就是第一个划分属性,其后依次类推,这就得到了决策树的形状,也就是怎么“长”了。
如果不理解的,可以查看我分享的图片示例,结合我说的,包你看懂:
不过,信息增益有一个问题:对可取值数目较多的属性有所偏好,例如:考虑将“编号”作为一个属性。为了解决这个问题,引出了另一个 算法C4.5。
为了解决信息增益的问题,引入一个信息增益率:
其中:
属性a的可能取值数目越多(即V越大),则IV(a)的值通常就越大。信息增益比本质: 是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大。不过有一个缺点:
使用信息增益率:基于以上缺点,并不是直接选择信息增益率最大的特征,而是现在候选特征中找出信息增益高于平均水平的特征,然后在这些特征中再选择信息增益率最高的特征。
数学家真实聪明,想到了另外一个表示纯度的方法,叫做基尼指数(讨厌的公式):

表示在样本集合中一个随机选中的样本被分错的概率。举例来说,现在一个袋子里有3种颜色的球若干个,伸手进去掏出2个球,颜色不一样的概率,这下明白了吧。Gini(D)越小,数据集D的纯度越高。
假设现在有特征 “学历”,此特征有三个特征取值: “本科”,“硕士”, “博士”,
当使用“学历”这个特征对样本集合D进行划分时,划分值分别有三个,因而有三种划分的可能集合,划分后的子集如下:
1.划分点: “本科”,划分后的子集合 : {本科},{硕士,博士}
2.划分点: “硕士”,划分后的子集合 : {硕士},{本科,博士}
3.划分点: “硕士”,划分后的子集合 : {博士},{本科,硕士}}
对于上述的每一种划分,都可以计算出基于 划分特征= 某个特征值 将样本集合D划分为两个子集的纯度:
因而对于一个具有多个取值(超过2个)的特征,需要计算以每一个取值作为划分点,对样本D划分之后子集的纯度Gini(D,Ai),(其中Ai 表示特征A的可能取值)
然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分,这个划分的划分点,便是使用特征A对样本集合D进行划分的最佳划分点。到此就可以长成一棵“大树”了。
ID3:取值多的属性,更容易使数据更纯,其信息增益更大。
训练得到的是一棵庞大且深度浅的树:不合理。
C4.5:采用信息增益率替代信息增益。
CART:以基尼系数替代熵,最小化不纯度,而不是最大化信息增益。
因为数值缩放不影响分裂点位置,对树模型的结构不造成影响。
按照特征值进行排序的,排序的顺序不变,那么所属的分支以及分裂点就不会有不同。而且,树模型是不能进行梯度下降的,因为构建树模型(回归树)寻找最优点时是通过寻找最优分裂点完成的,因此树模型是阶跃的,阶跃点是不可导的,并且求导没意义,也就不需要归一化。
既然树形结构(如决策树、RF)不需要归一化,那为何非树形结构比如Adaboost、SVM、LR、Knn、KMeans之类则需要归一化。
对于线性模型,特征值差别很大时,运用梯度下降的时候,损失等高线是椭圆形,需要进行多次迭代才能到达最优点。
但是如果进行了归一化,那么等高线就是圆形的,促使SGD往原点迭代,从而导致需要的迭代次数较少。
Classification And Regression Tree(CART)是决策树的一种,CART算法既可以用于创建分类树(Classification Tree),也可以用于创建回归树(Regression Tree),两者在建树的过程稍有差异。
回归树:
CART回归树是假设树为二叉树,通过不断将特征进行分裂。比如当前树结点是基于第j个特征值进行分裂的,设该特征值小于s的样本划分为左子树,大于s的样本划分为右子树。
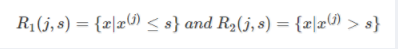
而CART回归树实质上就是在该特征维度对样本空间进行划分,而这种空间划分的优化是一种NP难问题,因此,在决策树模型中是使用启发式方法解决。典型CART回归树产生的目标函数为:
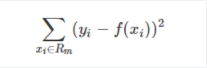
因此,当我们为了求解最优的切分特征j和最优的切分点s,就转化为求解这么一个目标函数:
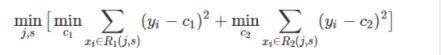
所以我们只要遍历所有特征的的所有切分点,就能找到最优的切分特征和切分点。最终得到一棵回归树。
决策树的剪枝基本策略有 预剪枝 (Pre-Pruning) 和 后剪枝 (Post-Pruning)。
参考文章:决策树及决策树生成与剪枝
作者:@mantchs
Update your browser to view this website correctly. Update my browser now