算法
5 分钟 读完 (大约 738 个字)

118. 杨辉三角

杨辉三角

题目

给定一个非负整数 numRows，生成杨辉三角的前 numRows行。

杨辉三角

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

1
2
3
4
5
6
7
8
9
输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

题解

  1. 动态规划

思路

如果能够知道一行杨辉三角，我们就可以根据每对相邻的值轻松地计算出它的下一行。

算法

虽然这一算法非常简单，但用于构造杨辉三角的迭代方法可以归类为动态规划，因为我们需要基于前一行来构造每一行。

首先，我们会生成整个 triangle 列表，三角形的每一行都以子列表的形式存储。然后，我们会检查行数为 0 的特殊情况，否则我们会返回 [1]。如果 numRows > 0，那么我们用 [1] 作为第一行来初始化 triangle with [1]，并按如下方式继续填充：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public List<List<Integer>> generate(int numRows) {
        List<List<Integer>> triangle = new ArrayList<List<Integer>>();

        // First base case; if user requests zero rows, they get zero rows.
        if (numRows == 0) {
            return triangle;
        }

        // Second base case; first row is always [1].
        triangle.add(new ArrayList<>());
        triangle.get(0).add(1);

        for (int rowNum = 1; rowNum < numRows; rowNum++) {
            List<Integer> row = new ArrayList<>();
            List<Integer> prevRow = triangle.get(rowNum-1);

            // The first row element is always 1.
            row.add(1);

            // Each triangle element (other than the first and last of each row)
            // is equal to the sum of the elements above-and-to-the-left and
            // above-and-to-the-right.
            for (int j = 1; j < rowNum; j++) {
                row.add(prevRow.get(j-1) + prevRow.get(j));
            }

            // The last row element is always 1.
            row.add(1);

            triangle.add(row);
        }

        return triangle;
    }
}

复杂度分析

  • 时间复杂度： O(numRows²)

虽然更新 triangle 中的每个值都是在常量时间内发生的，
但它会被执行 O(numRows²) 次。想要了解原因，就需要考虑总共有多少次循环迭代。很明显外层循环需要运行 numRows 次，但在外层循环的每次迭代中，内层循环要运行 rowNumrowNum 次。因此，triangle 发生的更新总数为
1 + 2 + 3 + ... + *numRows*，根据高斯公式有

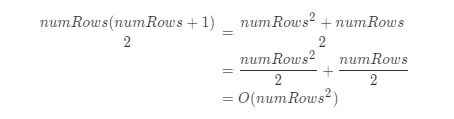
image.png

  • 空间复杂度：O(numRows²)

因为我们需要存储我们在 triangle 中更新的每个数字，
所以空间需求与时间复杂度相同。

  1. Python解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def generate(self, num_rows):
        triangle = []

        for row_num in range(num_rows):
            # The first and last row elements are always 1.
            row = [None for _ in range(row_num+1)]
            row[0], row[-1] = 1, 1

            # Each triangle element is equal to the sum of the elements
            # above-and-to-the-left and above-and-to-the-right.
            for j in range(1, len(row)-1):
                row[j] = triangle[row_num-1][j-1] + triangle[row_num-1][j]

            triangle.append(row)

        return triangle
  1. 递归解法

通过numRows-1，求numRows行，递归求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    List<List<Integer>> listw = new ArrayList<List<Integer>>();

    public List<List<Integer>> generate(int numRows) {
        List<Integer> listn = new ArrayList<Integer>();
        if (numRows == 0)
            return listw;
        generate(numRows - 1);
        for (int i = 0; i < numRows; i++) {
            if (i == 0) {
                listn.add(1);
                continue;
            } else if (i == numRows - 1) {
                listn.add(1);
                continue;
            } else if (i == numRows - 2) {
                listn.add(listw.get(numRows - 2).get(i - 1) + 1);
                continue;
            } else {
                listn.add(listw.get(numRows - 2).get(i - 1) + listw.get(numRows - 2).get(i));
            }
        }
        listw.add(listn);
        return listw;
    }
}
算法
3 分钟 读完 (大约 385 个字)

24. 两两交换链表中的节点

image.png

24. 两两交换链表中的节点

题目

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例:

给定 1->2->3->4, 你应该返回 2->1->4->3.

题解

  1. 非递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode pre = new ListNode(0);
        pre.next = head;
        ListNode temp = pre;
        while(temp.next != null && temp.next.next != null) {
            ListNode start = temp.next;
            ListNode end = temp.next.next;
            temp.next = end;
            start.next = end.next;
            end.next = start;
            temp = start;
        }
        return pre.next;
    }
}

  1. 递归解法

    1. 详细介绍一下递归的思路;
    2. 递归和栈处理问题类似,先把问题从前往后收集起来,然后再从后往前处理每一个问题;
    3. 两两交换链表结点,先处理最后两个或一个节点,然后再从后往前处理每一对节点;
    4. 先创建一个next临时结点保存head的下一个结点,然后让head指向下下一个节点,最后让 next节点指向head结点;
    5. 此题只有处理完后面的结点才可处理前面的结点,画图更容易理解;

image.png

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null)
            return head;

        // 三个节点顺序:head, next, swapPairs(next.next)
        ListNode next = head.next;
        head.next = swapPairs(next.next);
        next.next = head;
        return next;
    }
}
算法
2 分钟 读完 (大约 323 个字)

334. 反转字符串

image.png

334. 反转字符串

题目

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

示例 1：

输入：["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

题解

  1. 递归解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public void reverseString(char[] s) {
        swap(0, s.length-1, s);
    }
    
    public void swap(int start, int end, char[] s) {
        if(start >= end){
            return;
        }
        char temp = s[start];
        s[start] = s[end];
        s[end] = temp;
        swap(start+1, end-1, s);
    }
}
  1. 循环解法
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public void reverseString(char[] s) {
        int j=s.length-1;
        for(int i=0;i<s.length/2;i++){
            char tmp = s[i];
            s[i] = s[j];
            s[j] = tmp;
            j--;
        }
    }
}
  1. Python解法
1
2
def reverseString(self, s: List[str]) -> None:
    s[0::]=s[::-1]
  1. c++解法

双指针，交换头尾两个指针所指的两个位置的值，指针向中间移动一个位置，重复以上操作，直到两个指针交错；

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    void reverseString(vector<char>& s) {
        int i = 0;
        int j = s.size() - 1;
        while(i<j)
        {
            swap(s[i],s[j]);
            ++ i;
            -- j;
        }
    }
};
关注我

链接

分类

最新文章

最新文章

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×