
PythonRobotics
Python codes for robotics algorithm.
PaddlePaddle 提供了丰富的计算单元,使得用户可以采用模块化的方法解决各种学习问题。在此Repo中,我们展示了如何用 PaddlePaddle来解决常见的机器学习任务,提供若干种不同的易学易用的神经网络模型。PaddlePaddle用户可领取免费Tesla V100在线算力资源,高效训练模型,每日登陆即送12小时,连续五天运行再加送48小时,前往使用免费算力。

前言
总括: 本文详细讲述了RSA算法详解,包括内部使用数学原理以及产生的过程。
原文博客地址:RSA算法详解
知乎专栏&&简书专题:前端进击者(知乎)&&前端进击者(简书)
博主博客地址:Damonare的个人博客
相濡以沫。到底需要爱淡如水。
正文
之前写过一篇文章SSL协议之数据加密过程,里面详细讲述了数据加密的过程以及需要的算法。SSL协议很巧妙的利用对称加密和非对称加密两种算法来对数据进行加密。这篇文章主要是针对一种最常见的非对称加密算法——RSA算法进行讲解。其实也就是对私钥和公钥产生的一种方式进行描述。首先先来了解下这个算法的历史:
RSA是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。
但实际上,在1973年,在英国政府通讯总部工作的数学家克利福德·柯克斯(Clifford Cocks)在一个内部文件中提出了一个相同的算法,但他的发现被列入机密,一直到1997年才被发表。
所以谁是RSA算法的发明人呢?不好说,就好像贝尔并不是第一个发明电话的人但大家都记住的是贝尔一样,这个地方我们作为旁观者倒不用较真,重要的是这个算法的内容:
RSA算法用到的数学知识特别多,所以在中间介绍这个算法生成私钥和公钥的过程中会穿插一些数学知识。生成步骤如下:
什么是质数?我想可能会有一部分人已经忘记了,定义如下:
除了1和该数自身外,无法被其他自然数整除的数(也可定义为只有1该数本身两个正因数]的数)。
比如2,3,5,7这些都是质数,9就不是了,因为3*3=9了
这里的数学概念就是什么是欧拉函数了,什么是欧拉函数呢?
欧拉函数的定义:
欧拉函数 φ(n)是小于或等于n的正整数中与n互质的数的数目。
互质的定义:
如果两个或两个以上的整数的最大公约数是 1,则称它们为互质
例如:φ(8) = 4,因为1,3,5,7均和8互质。
推导欧拉函数:
(1)如果n = 1, φ(1) = 1;(小于等于1的正整数中唯一和1互质的数就是1本身);
(2)如果n为质数,φ(n) = n - 1;因为质数和每一个比它小的数字都互质。比如5,比它小的正整数1,2,3,4都和他互质;
(3) 如果n是a的k次幂,则 φ(n) = φ(a^k) = a^k - a^(k-1) = (a-1)a^(k-1);
(4) 若m,n互质,则φ(mn) = φ(m)φ(n)
证明:设A, B, C是跟m, n, mn互质的数的集,据中国剩余定理(经常看数学典故的童鞋应该了解,剩余定理又叫韩信点兵,也叫孙子定理),A*B和C可建立双射一一对应)的关系。(或者也可以从初等代数角度给出欧拉函数积性的简单证明) 因此的φ(n)值使用算术基本定理便知。(来自维基百科)
模反元素:
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1。
比如3和5互质,3关于5的模反元素就可能是2,因为32-1=5可以被5整除。所以很明显模反元素不止一个,2加减5的整数倍都是3关于5的模反元素{…-3, 2,7,12…}* 放在公式里就是3*2 = 1 (mod 5)
上面所提到的欧拉函数用处实际上在于欧拉定理:
欧拉定理:
如果两个正整数a和n互质,则n的欧拉函数 φ(n) 可以让下面的等式成立:
a^φ(n) = 1(mod n)
由此可得:a的φ(n - 1)次方肯定是a关于n的模反元素。
欧拉定理就可以用来证明模反元素必然存在。
由模反元素的定义和欧拉定理我们知道,a的φ(n)次方减去1,可以被n整除。比如,3和5互质,而5的欧拉函数φ(5)等于4,所以3的4次方(81)减去1,可以被5整除(80/5=16)。
小费马定理:
假设正整数a与质数p互质,因为质数p的φ(p)等于p-1,则欧拉定理可以写成
a^(p-1) = 1 (mod p)
这其实是欧拉定理的一个特例。
我们知道像RSA这种非对称加密算法很安全,那么到底为啥子安全呢? 我们来看看上面这几个过程产生的几个数字:
p,q:我们随机挑选的两个大质数;
N:是由两个大质数p和q相乘得到的。N = p * q;
r:由欧拉函数得到的N的值,r = φ(N) = φ(p)φ(q) = (p-1)(q-1)。
e:随机选择和和r互质的数字,实际中通常选择65537;
d: d是以欧拉定理为基础求得的e关于r的模反元素,ed = 1 (mod r);
N和e我们都会公开使用,最为重要的就是私钥中的d,d一旦泄露,加密也就失去了意义。那么得到d的过程是如何的呢?如下:
比如知道e和r,因为d是e关于r的模反元素;r是φ(N) 的值
而φ(N)=(p-1)(q-1),所以知道p和q我们就能得到d;
N = pq,从公开的数据中我们只知道N和e,所以问题的关键就是对N做因式分解能不能得出p和q
所以得出了在上篇博客说到的结论,非对称加密的原理:
将a和b相乘得出乘积c很容易,但要是想要通过乘积c推导出a和b极难。即对一个大数进行因式分解极难
目前公开破译的位数是768位,实际使用一般是1024位或是2048位,所以理论上特别的安全。
后记
RSA算法的核心就是欧拉定理,根据它我们才能得到私钥,从而保证整个通信的安全。
给定整数 n 和 k,找到 1 到 n 中字典序第 k 小的数字。
注意:1 ≤ k ≤ n ≤ 109。
示例 :
1 | 输入: |
乍一看这一题貌似毫无头绪,什么是字典序?如何定位这个数?没错,刚接触这个题目的时候,我的脑筋里也是一团乱麻。
但是我觉得作为一个拥有聪明才智的程序员来说,最重要的能力就是迅速抽象问题、拆解问题的能力。经过一段时间的思考,我的脑筋里还是没有答案。
哈哈。
言归正传,我们来分析一下这个问题。
首先,什么是字典序?
什么是字典序?
简而言之,就是根据数字的前缀进行排序,
比如10 < 9,因为10的前缀是1,比9小,
再比如112 < 12,因为112的前缀11小于12。
这样排序下来,会跟平常的升序排序会有非常大的不同。先给你一个直观的感受,一个数乘10,或者加1,哪个大?可能你会吃惊,后者会更大。
但其实掌握它的本质之后,你一点都不会吃惊。
问题建模
画一个图你就懂了。
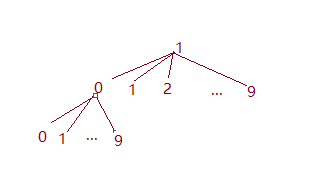
每一个节点都拥有10个孩子节点,因为作为一个前缀 ,它后面可以接0~9这十个数字。而且你可以非常容易地发现,整个字典序排列也就是对十叉树进行层序遍历。1, 10, 11, 12, 13 … 100, 101, …
回到题目的意思,我们需要找到排在第k位的数。找到他的排位,需要搞清楚三件事情:
怎么确定一个前缀下所有子节点的个数?
如果第k个数在当前的前缀下,怎么继续往下面的子节点找?
如果第k个数不在当前的前缀,即当前的前缀比较小,如何扩大前缀,增大寻找的范围?
接下来 ,我们一一拆解这些问题。
理顺思路
我们现在的思路就是用下一个前缀的起点减去当前前缀的起点,那么就是当前前缀下的所有子节点数总和啦。
1 | //prefix是前缀,n是上界 |
当然,不知道大家发现一个问题没有,当next的值大于上界的时候,那以这个前缀为根节点的十叉树就不是满十叉树了啊,应该到上界那里,后面都不再有子节点。因此,count += next - cur还是有些问题的,我们来修正这个问题:
1 | count += Math.max(n+1, next) - cur; |
你可能会问:咦?怎么是n+1,而不是n呢?不是说好了n是上界吗?
我举个例子,假若现在上界n为12,算出以1为前缀的子节点数,首先1本身是一个节点,接下来要算下面10,11,12,一共有4个子节点。
那么如果用Math.max(n, next) - cur会怎么样?
这时候算出来会少一个,12 - 10加上根节点,最后只有3个。因此我们务必要写n+1。
现在,我们搞定了前缀的子节点数问题。
prefix这样处理就可以了。
1 | prefix *= 10 |
3.第k个数不在当前前缀下
说白了,当前的前缀小了嘛,我们扩大前缀。
1 | prefix ++; |
框架搭建
整合一下刚刚的思路。
1 | let findKthNumber = function(n, k) { |
完整代码展示
1 | /** |
1 | public class Solution { |
红黑树本质上是一种二叉查找树,但它在二叉查找树的基础上额外添加了一个标记(颜色),同时具有一定的规则。这些规则使红黑树保证了一种平衡,插入、删除、查找的最坏时间复杂度都为 O(logn)。
它的统计性能要好于平衡二叉树(AVL树),因此,红黑树在很多地方都有应用。比如在 Java 集合框架中,很多部分(HashMap, TreeMap, TreeSet 等)都有红黑树的应用,这些集合均提供了很好的性能。
由于 TreeMap 就是由红黑树实现的,因此本文将使用 TreeMap 的相关操作的代码进行分析、论证。
黑色高度
从根节点到叶节点的路径上黑色节点的个数,叫做树的黑色高度。
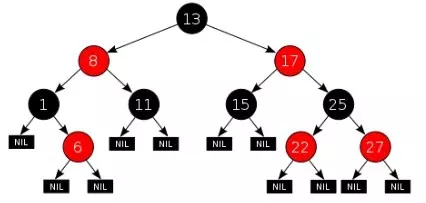
红黑树在原有的二叉查找树基础上增加了如下几个要求:
中文意思是:
注意:
性质 3 中指定红黑树的每个叶子节点都是空节点,而且并叶子节点都是黑色。但 Java 实现的红黑树将使用 null 来代表空节点,因此遍历红黑树时将看不到黑色的叶子节点,反而看到每个叶子节点都是红色的。
性质 4 的意思是:从每个根到节点的路径上不会有两个连续的红色节点,但黑色节点是可以连续的。
因此若给定黑色节点的个数 N,最短路径的情况是连续的 N 个黑色,树的高度为 N - 1;最长路径的情况为节点红黑相间,树的高度为 2(N - 1) 。
性质 5 是成为红黑树最主要的条件,后序的插入、删除操作都是为了遵守这个规定。
红黑树并不是标准平衡二叉树,它以性质 5 作为一种平衡方法,使自己的性能得到了提升。

红黑树的左右旋是比较重要的操作,左右旋的目的是调整红黑节点结构,转移黑色节点位置,使其在进行插入、删除后仍能保持红黑树的 5 条性质。
比如 X 左旋(右图转成左图)的结果,是让在 Y 左子树的黑色节点跑到 X 右子树去。
我们以 Java 集合框架中的 TreeMap 中的代码来看下左右旋的具体操作方法:
指定节点 x 的左旋 (右图转成左图):
1 | //这里 p 代表 x |
可以看到,x 节点的左旋就是把 x 变成 右孩子 y 的左孩子,同时把 y 的左孩子送给 x 当右子树。
简单点记就是:左旋把右子树里的一个节点(上图 β)移动到了左子树。
指定节点 y 的右旋(左图转成右图):
1 | private void rotateRight(Entry p) { |
同理,y 节点的右旋就是把 y 变成 左孩子 x 的右孩子,同时把 x 的右孩子送给 x 当左子树。
简单点记就是:右旋把左子树里的一个节点(上图 β)移动到了右子树。
了解左旋、右旋的方法及意义后,就可以了解红黑树的主要操作:插入、删除。
红黑树并不是真正的平衡二叉树,但在实际应用中,红黑树的统计性能要高于平衡二叉树,但极端性能略差。
红黑树的插入、删除调整逻辑比较复杂,但最终目的是满足红黑树的 5 个特性,尤其是 4 和 5。
在插入调整时为了简化操作我们直接把插入的节点涂成红色,这样只要保证插入节点的父节点不是红色就可以了。
而在删除后的调整中,针对删除黑色节点,所在子树缺少一个节点,需要进行弥补或者对别人造成一个黑色节点的伤害。具体调整方法取决于兄弟节点所在子树的情况。
红黑树的插入、删除在树形数据结构中算比较复杂的,理解起来比较难,但只要记住,红黑树有其特殊的平衡规则,而我们为了维持平衡,根据邻树的状况进行旋转或者涂色。
红黑树这么难理解,必定有其过人之处。它的有序、快速特性在很多场景下都有用到,比如 Java 集合框架的 TreeMap, TreeSet 等。

题目描述
现在有一棵合法的二叉树,树的节点都是用数字表示,现在给定这棵树上所有的父子关系,求这棵树的高度
时间限制C/C++语言:1000MS 其它语言:3000MS
内存限制C/C++语言:65536KB 其它语言:589824KB
输入
输入的第一行表示节点的个数n(1<=n<=1000,节点的编号为0到n-1)组成,下面是n-1行,每行有两个整数,第一个数表示父节点的编号,第二个数表示子节点的编号
输出
输出树的高度,为一个整数
样例输入
1 | 5 |
样例输出
1 | 3 |
java
1 | import java.util.Scanner; |
python
1 | import sys |
javascript
1 | var n=readInt(),rec={},dps={},rs=1 |
一个天平上有6个位置,左右各三个位置,有6个砝码,分别是1、2、3、4、5、6克重。
要使天平平衡,有多少种方法?(对称摆放算作一种方法)
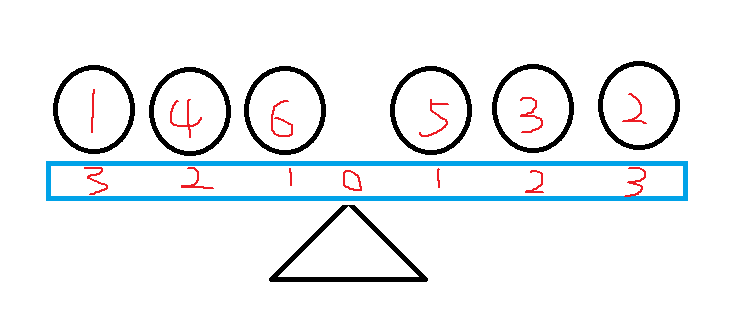
暴力求解
1 | #include <iostream> |
1 | 1 4 6 | 5 3 2 |
给定一个非负整数 numRows,生成杨辉三角的前 numRows行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
1 | 输入: 5 |
思路
如果能够知道一行杨辉三角,我们就可以根据每对相邻的值轻松地计算出它的下一行。
算法
虽然这一算法非常简单,但用于构造杨辉三角的迭代方法可以归类为动态规划,因为我们需要基于前一行来构造每一行。
首先,我们会生成整个 triangle 列表,三角形的每一行都以子列表的形式存储。然后,我们会检查行数为 0 的特殊情况,否则我们会返回 [1]。如果 numRows > 0,那么我们用 [1] 作为第一行来初始化 triangle with [1],并按如下方式继续填充:
1 | class Solution { |
复杂度分析
虽然更新 triangle 中的每个值都是在常量时间内发生的,
但它会被执行 O(numRows²) 次。想要了解原因,就需要考虑总共有多少次循环迭代。很明显外层循环需要运行 numRows 次,但在外层循环的每次迭代中,内层循环要运行 rowNumrowNum 次。因此,triangle 发生的更新总数为1 + 2 + 3 + ... + *numRows*,根据高斯公式有
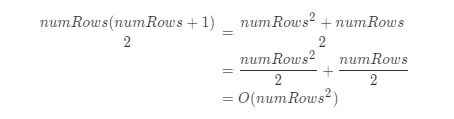
因为我们需要存储我们在 triangle 中更新的每个数字,
所以空间需求与时间复杂度相同。
1 | class Solution: |
通过numRows-1,求numRows行,递归求解
1 | class Solution { |
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例:
给定 1->2->3->4, 你应该返回 2->1->4->3.1 | /** |
递归解法
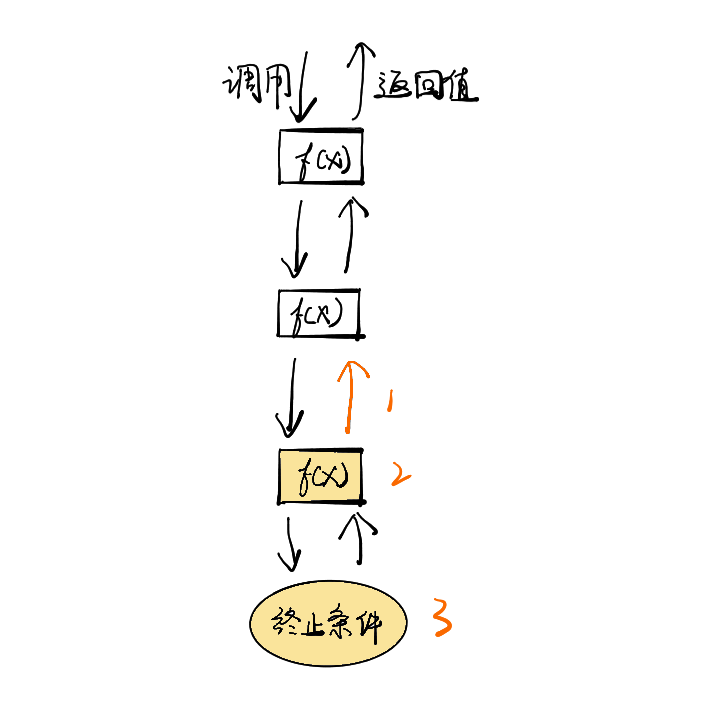
1 | class Solution { |
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:["h","e","l","l","o"]
输出:["o","l","l","e","h"]示例 2:
输入:["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"] 1 | class Solution { |
1 | class Solution { |
1 | def reverseString(self, s: List[str]) -> None: |
双指针,交换头尾两个指针所指的两个位置的值,指针向中间移动一个位置,重复以上操作,直到两个指针交错;
1 | class Solution { |

作者:程序汪追风
链接:https://juejin.im/post/5d5fd40bf265da03df5f1b3a
来源:掘金
Update your browser to view this website correctly. Update my browser now