2019-09-17

算法

10 分钟读完 (大约 1556 个字) 0次访问

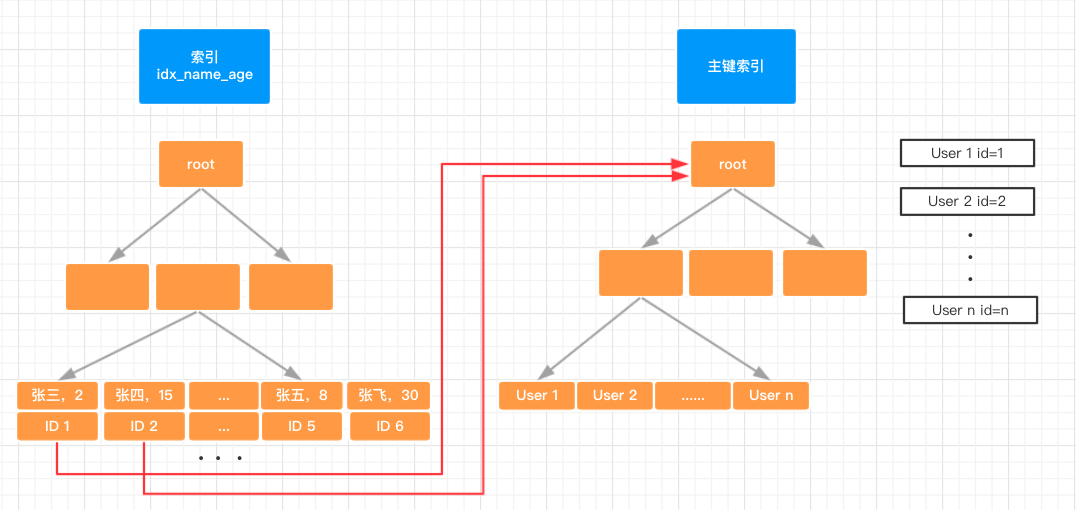
440. 字典序的第K小数字

题目

给定整数 n 和 k，找到 1 到 n 中字典序第 k 小的数字。

注意：1 ≤ k ≤ n ≤ 109。

示例 :

输入:
n: 13   k: 2

输出:
10

解释:
字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9]，所以第二小的数字是 10。

题解

乍一看这一题貌似毫无头绪，什么是字典序？如何定位这个数？没错，刚接触这个题目的时候，我的脑筋里也是一团乱麻。

但是我觉得作为一个拥有聪明才智的程序员来说，最重要的能力就是迅速抽象问题、拆解问题的能力。经过一段时间的思考，我的脑筋里还是没有答案。

哈哈。

言归正传，我们来分析一下这个问题。

首先，什么是字典序？

什么是字典序？
简而言之，就是根据数字的前缀进行排序，

比如10 < 9，因为10的前缀是1，比9小，

再比如112 < 12，因为112的前缀11小于12。

这样排序下来，会跟平常的升序排序会有非常大的不同。先给你一个直观的感受，一个数乘10，或者加1，哪个大？可能你会吃惊，后者会更大。

但其实掌握它的本质之后，你一点都不会吃惊。

问题建模
画一个图你就懂了。

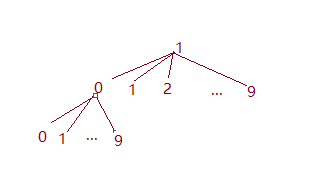
每一个节点都拥有10个孩子节点，因为作为一个前缀，它后面可以接0~9这十个数字。而且你可以非常容易地发现，整个字典序排列也就是对十叉树进行层序遍历。1, 10, 11, 12, 13 … 100, 101, …

回到题目的意思，我们需要找到排在第k位的数。找到他的排位，需要搞清楚三件事情:

怎么确定一个前缀下所有子节点的个数？
如果第k个数在当前的前缀下，怎么继续往下面的子节点找？
如果第k个数不在当前的前缀，即当前的前缀比较小，如何扩大前缀，增大寻找的范围？
接下来，我们一一拆解这些问题。

理顺思路

确定指定前缀下所有子节点数
现在的任务就是给定一个前缀，返回下面子节点总数。

我们现在的思路就是用下一个前缀的起点减去当前前缀的起点，那么就是当前前缀下的所有子节点数总和啦。

//prefix是前缀，n是上界
var getCount = (prefix, n) => {
    let cur = prefix;
    let next = prefix + 1;//下一个前缀
    let count = 0;
    //当前的前缀当然不能大于上界
    while(cur <= n) {
        count += next - cur;//下一个前缀的起点减去当前前缀的起点
        cur *= 10; 
        next *= 10;
        // 如果说刚刚prefix是1，next是2，那么现在分别变成10和20
        // 1为前缀的子节点增加10个，十叉树增加一层, 变成了两层
        
        // 如果说现在prefix是10，next是20，那么现在分别变成100和200，
        // 1为前缀的子节点增加100个，十叉树又增加了一层，变成了三层
    }
    return count;//把当前前缀下的子节点和返回去。
}

当然，不知道大家发现一个问题没有，当next的值大于上界的时候，那以这个前缀为根节点的十叉树就不是满十叉树了啊，应该到上界那里，后面都不再有子节点。因此，count += next - cur还是有些问题的，我们来修正这个问题:

1	count += Math.max(n+1, next) - cur;

你可能会问:咦？怎么是n+1,而不是n呢？不是说好了n是上界吗？

我举个例子，假若现在上界n为12，算出以1为前缀的子节点数，首先1本身是一个节点，接下来要算下面10，11，12，一共有4个子节点。

那么如果用Math.max(n, next) - cur会怎么样？

这时候算出来会少一个，12 - 10加上根节点，最后只有3个。因此我们务必要写n+1。

现在，我们搞定了前缀的子节点数问题。

第k个数在当前前缀下
现在无非就是往子树里面去看。

prefix这样处理就可以了。

1	prefix *= 10

3.第k个数不在当前前缀下
说白了，当前的前缀小了嘛，我们扩大前缀。

1	prefix ++;

框架搭建
整合一下刚刚的思路。

let findKthNumber = function(n, k) {
  let p = 1;//作为一个指针，指向当前所在位置，当p==k时，也就是到了排位第k的数
  let prefix = 1;//前缀
  while(p < k) {
    let count = getNumber(prefix, n);//获得当前前缀下所有子节点的和
    if(p + count > k) { //第k个数在当前前缀下
      prefix *= 10;
      p++; //把指针指向了第一个子节点的位置，比如11乘10后变成110，指针从11指向了110
    } else if(p + count <= k) { //第k个数不在当前前缀下
      prefix ++;
      p += count;//注意这里的操作，把指针指向了下一前缀的起点
    }
  }
  return prefix;
};

完整代码展示

/**
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var findKthNumber = function(n, k) {
  let getCount = (prefix, n) => {
    let count =  0;
    for(let cur = prefix, next = prefix + 1; cur <= n; cur *= 10, next *= 10) 
      count += Math.min(next, n+1) - cur;
    return count;
  }
  let p = 1;
  let prefix = 1;
  while(p < k) {
    let count = getCount(prefix, n);
    if(p + count > k) {
      prefix *= 10;
      p++;
    } else if(p + count <= k) {
      prefix ++;
      p += count;
    }
  }
  return prefix;
};

public class Solution {
    /**
     * @param n: a integer
     * @param k: a integer
     * @return: return a integer
     */
    public int findKthNumber(int n, int k) {
        int curr = 1;
        k = k - 1;
        while (k > 0) {
            int steps = calSteps(n, curr, curr + 1);
            if (steps <= k) {   //如果不在当前层，减去steps
                curr += 1;      
                k -= steps;  
            } 
            else {              //说明在当前层,curr*10缩小搜索范围继续查找
                curr *= 10;
                k -= 1;
            }
        }
        return curr;
    }
    //use long in case of overflow
    public int calSteps(int n, long n1, long n2) { //计算curr开头和curr+1开头之间的字符串数量
        int steps = 0;
        while (n1 <= n) {
            steps += Math.min(n + 1, n2) - n1;  //每次加上当前的字符串数量
            n1 *= 10;       //每次均扩大10倍
            n2 *= 10;
        }
        return steps;
    }
}

# leetcode, 算法

440. 字典序的第K小数字

440. 字典序的第K小数字

题目

题解

喜欢这篇文章？打赏一下作者吧

评论

链接

分类

最新文章

最新文章

Your browser is out-of-date!