相对论
光线在通过强引力场附近时会发生弯曲,这是广义相对论的重要预言之一

如果我说,相对论与日常生用息息相关,你会信吗?或许就算我是一位知名的物理学教授,说服力相信也不会大得多少。以下我将要用比较浅白简单的文字和少许初等代数,说明并说服大家,相对论并不难懂,而且它在日常经验中是如此的明显、如此的必要!
1905 年被称为爱因斯坦的「奇迹年」,爱因斯坦向世界提出了一套非常明显、非常合理,但却一直不为人所理解的理论狭义相对论(special relativity)。被称为「狭义」是因为这个理论只在惯性座标系中适用;换句话说,即是在所有没有加速度的系统中都适用。狭义相对论建基于两大假设:
- 在所有的惯性系统中,所有有物理定律保持不变。
- 对于所有系统中的所有观测者,光速永远不变,而且不是无限快的。
假设(一)「所有自然定律不变」一般被称为相对性原理(principle of relativity),明显比较合理,也比较容易理解。而乍看之下,光速相对于所有人都不变,而不论那人正在高速奔跑或者静止不动都没有关系,就显得较为奇怪了。要理解这一点,我们需要由速度的意义说起。速度,就是在说「每单位时间内走了多远」。说得再浅白一点,可以想像为「每秒走了多少米(m/s)」。但这只是惯用单位的问题,你当然可以想成「每小时走了多少公里(km/h)」,这正是司机们惯用的单位。在科学中,单位是至关重要的,因为不同单位的东西就是不同性质的东西,不可以混为一谈的比较,好像一个苹果永远不会等于一个橙。
假设(二)「光速相对所有人都不变」,就是说相对于所有人,光在每单位时间内走的距离都一样。就是说,当你向着一道光奔跑,「直觉上」你会认为你所看到的光速比起你在静止不动时快,因为在你向光跑去的「同时」,光亦向着你冲去。换成数学上的表达,就是说如果你用速度 v 向着光冲去,而我们用 c 代表你在静止时看到的光速,那你看到的光速就会变成了c + v。这就是所谓的伽俐略变换,亦被一般人叫做「常识」。当然了啊,两个物件互相冲去,当然会比其中一个不动、或两者互相远离快啊。但是,爱因斯坦却说不论你用什么速度,向着光或离开光移动,你到的光速都仍然为 c,不多也不少!
你会说:「这怎可能!这是违反常识的!」我的回答是,一般人的常识存在非常明显的漏洞,可是在爱因斯坦之前却一直没有人留意到这个严重的错误!这个错误就是「同时」这一概念的演绎。什么是「同时」?就是说大家的时钟显示的时间都一样啊!对,这也是爱因斯坦对「同时」的理解。但现在要再问一道问题,如何知道两个时钟的时间一样?
问题到肉了,可是你会觉得很无聊:「说什么废话!只要我看到两个钟的指针拍着的时间就是了!」好,停一停,想一想:我们能「看」到东西,是因为光进入到我们的眼球穿过水晶体折射后投影在视网膜上。总言之,我们能看到东西,是因为有光。光以一定的速度前进,而且因为光速有限,因此在不同距离发出的光相对于同一个观测者而言,会在不同时间到达。试想像,两个人相距非常远,而两个人都带着一个时钟,那么当然,任何一方都会觉得对方那个时钟所发出的光,会比自己手上的时钟所发出的光要用更多时间才能进入你的眼睛吧!好了,我希望大家想想,究竟事先要如何调整两个时钟,才能使你和对方都看到两个时钟是同步的呢?当然,这是办不到的!因为两个时钟相距两个人的距离都不同。若然你看到它们是同步的,对方就会看到他手上的走得较快,反之亦然。
如果你不太理解的话,请从头思考一次,先不要跳过读下去,因为刚才所说的就是相对论的精髓所在。重点是,要知道世界上并没有「对所有人都同时」这个概念存在,因此也可以说,「同时」这个概念对每个人都不同;说「对大家来说都是同时」就是错误的,没有可能发生。这是非常明显的,但却一直被我们所忽略。这完全是因为对于人类的感觉来说,光速(每秒三十万公里,能够环绕地球七个半圈) 实在是太快、太快了。
好了,接下来我要介绍相对论导致的两个非常重要的结果,这些结果令人类对时间及空间的概念有了根本上的改变:时间及空间其实是互相纠缠、难分难离的。在这部分我会以数学论证,狭义相对论所涉及的数学都只是基本数学运算以及向量微积分,相信对有会考物理根基的朋友来说不会太难。
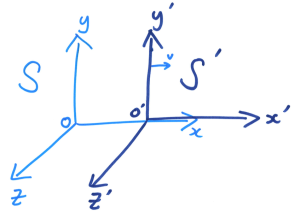
在我们生活的三维空间中,每一件事件都可以用座标系的四个变量决定,就是(长,阔,高,时间),数学表达为( x , y , z , t )。假设在座标系 S 中有一原点 O,在 S 内观测的人都会对每一件事件测得一组座标( x , y , z , t );而现在有另一座标系S’正在相对S以速度 v 向右移动,它的原点 O’ 在时间 t = 0的时候刚好与 O重叠,而在S’内观测的人都会对每一件事件测得一组座标( x’ , y’ , z’ , t’ )。那么,在我们的「常识」中, ( x , y , z , t )与 ( x’ , y’ , z’ , t’ )的关系就是由伽俐略变换来决定:
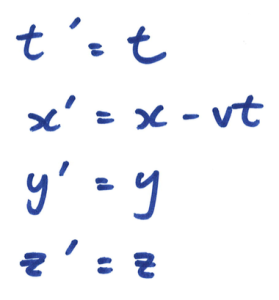
这就是我们认为的「常识」的数学表达方法。留意当中t’ = t,因为在传统的观念里,「同时」这概念仍然存在。明显地,在伽俐略变换当中,时间是独立地流逝的,与空间( x , y , z )无关。可是,在上文中我们知道「同时」是不存在的。
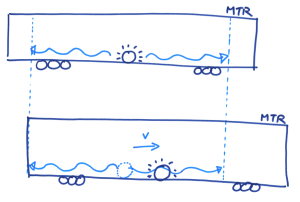
想像小明站在一节正在行进的列车车厢正中间,在车头及车尾都摆放了感应器。他向左右同时照射出两道光束。对小明来说,车厢并没有移动,所以他会看到两道光束同时到达感应器。可是,对于一位站在月台上的人来说,因为列车正在向右移动,右边的感应器不断远离光束,而左边的就不断靠边光束。所以他会看到左边那道光束首先到达感应器。因此,时间会因为观测者的运动状态不同而有所分别,而且这是非常明显的!请注意,上述两种情况都是正确的,没有谁对谁错,完全因为观点与角度而已。回到 S 和 S’ 座标系的讨论,因为两个座标系的运动状态不同,所以伽俐略变换就不是正确的描述了,我们必须改用另外一种座标变换方法,名为洛伦兹变换( Lorentz Transformation):
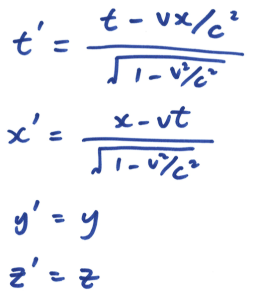
有关这组公式的推导过程,有兴趣的朋友可以参考任何相对论课本。在这里我们有兴趣的是:如果时间及空间确实根据以上方程组变换的话,会有什么有趣的事情发生?
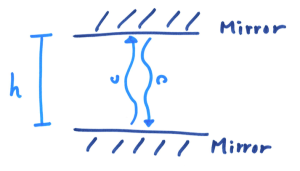
首先,考虑一个「光钟」,这是一个纯粹由两块互相平行的平面镜组成的计时器,有一束光在两块镜之间来回反弹。然后我们定义这束光来回反弹一次的时间Δ t = 2 h / c 为一个时间单位,故此我们就有了这样一种有趣的计时器。
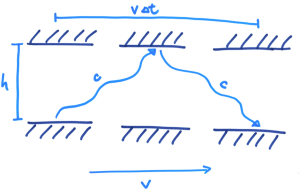
现在,我们让这个光钟在S座标系中以水平方向向右以均速 v 移动。所以我们就知道,如果我们称光钟为S’ 座标系,就有Δ t’ = 2 h / c。在S 座标系当中,光就是以斜线行进的,根据毕氐定理,我们得到
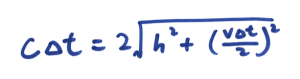
使用简单代数运算求得Δ t:
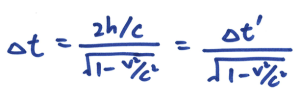
因为v < c,所以分母必定小于1 ,故此Δ t’ < Δ t。换句话说,移动中的座标系的时间流逝得比较慢。这就是著名的时间迟滞(Time Dilation) 。
除了移动中的人的时间在其他人眼中会变慢之外,移动中的物体看起来也会变短。这叫做长度收缩(Length Contraction)。如果L 0 是物体静止时的长度,L是物体相对于观测者以速度 v移动时的长度,那么我们就会得到
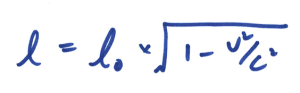
公式(3) 的推导过程与公式(2) 差不多,只要把光钟转个直角再考虑水平移动就可以了,有兴趣的朋友可以自己当做练习试试推导。
以上两个「违反直觉」的现象都已经被实验观测所证实了。其中一个重要的证明是关于宇宙射线的问题。每分每秒都有大量的宇宙射线攻击着地球,这些射线多是带电粒子诸如质子及电子等等,能量很高。幸好地球有磁场以及大气层的保护,不然地球上就不可能有生命存在了。
一些粒子与大气粒子碰撞后,会产生许多不同种类的粒子,向各个方向散射。这些粒子的寿命一般都非常短暂,就算在产生的一刻开始已经用接近光速前进,在它再衰变成其他粒子之前,前进的距离最多也只得几百米。但是,虽然地球的大气层厚度约为100公里,设置在地面上的仪器却可以探测到它们!这完全是因为这些粒子以接近光速行进,相对论的效应就会变得很大。如果在静止时这些粒子的寿命是 T,那么根据时间迟滞现象,地面上的人就会测得它们的寿命为
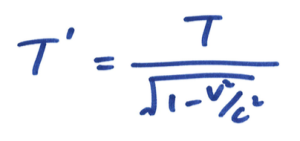
其中 v 是粒子的速度。明显地,当 v 非常接近 c 的时候,T’ 就会变得非常大,所以它们有足够的时间可以穿过厚厚的大气层落到地面。
我最后想介绍的是著名的爱因斯坦速度相加法则。在早前的讨论中,我们已经明白到,在光速不是无限快的条件下,时间必须是「相对」的。亦即是说,对于不同运动状态的观测者,时间的流逝速率各有不同。同样地对于空间来说也是如此。因此,我们就不能说两个互相靠近的人的相对速度 v’,会简单地为 v’ = v 1 + v 2,其中 v 1 和 v 2 分别为两个人的速度。那么 v’ 应该如何表达才对呢?其实简单得很,只要把洛伦兹公式对时间微分就可以了。详细的做法可以参考教科书,其结果为
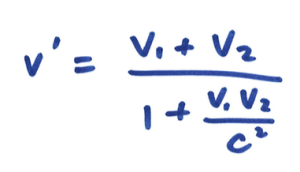
因此可以看到在相对论下,相对速度 v’ 比较小。如果代入文章开头的例子,你和光束互相冲向对方,就有
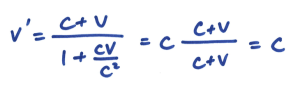
所以你会惊讶地发现,c + v 仍然是 c!这是当然的,因为相对论本身必须符合它的假设:光速不变。
其实狭义相对论还有许多有趣的题目可以讨论的,例如著名的质能公式E = mc^2、双生子悖论、能量-动量四维向量、以及相对论性电磁场理论等等,或许在以后我会和大家深入讨论。而爱因斯坦在1916 年提出的广义相对论(general relativity),则是一套把重力与加速度都包含在内的时空理论,能够非常准确地描述我们身处的宇宙。广义相对论所涉及的数学非常深奥,需要使用到十分抽象的黎曼几何以及张量的概念,确实并非每个学生也能明白。在以后我会试试为大家说明广义相对论的重要性。总而言之,在这篇文章中,我希望大家明白的事,是相对论其实并非一般人想像的那么深奥难懂。至少,就狭义相对论而言,只需要中学程度的物理及数学知识就可以了。