什么是红黑树
红黑树本质上是一种二叉查找树,但它在二叉查找树的基础上额外添加了一个标记(颜色),同时具有一定的规则。这些规则使红黑树保证了一种平衡,插入、删除、查找的最坏时间复杂度都为 O(logn)。
它的统计性能要好于平衡二叉树(AVL树),因此,红黑树在很多地方都有应用。比如在 Java 集合框架中,很多部分(HashMap, TreeMap, TreeSet 等)都有红黑树的应用,这些集合均提供了很好的性能。
由于 TreeMap 就是由红黑树实现的,因此本文将使用 TreeMap 的相关操作的代码进行分析、论证。
黑色高度
从根节点到叶节点的路径上黑色节点的个数,叫做树的黑色高度。
红黑树的 5 个特性
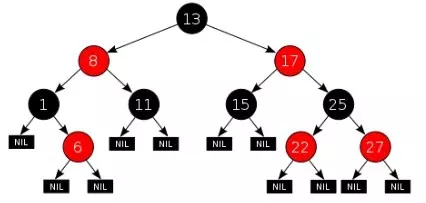
红黑树在原有的二叉查找树基础上增加了如下几个要求:
- Every node is either red or black.
- The root is black.
- Every leaf (NIL) is black.
- If a node is red, then both its children are black.
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
中文意思是:
- 每个节点要么是红色,要么是黑色;
- 根节点永远是黑色的;
- 所有的叶节点都是是黑色的(注意这里说叶子节点其实是上图中的 NIL 节点);
- 每个红色节点的两个子节点一定都是黑色;
- 从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点;
注意:
性质 3 中指定红黑树的每个叶子节点都是空节点,而且并叶子节点都是黑色。但 Java 实现的红黑树将使用 null 来代表空节点,因此遍历红黑树时将看不到黑色的叶子节点,反而看到每个叶子节点都是红色的。
性质 4 的意思是:从每个根到节点的路径上不会有两个连续的红色节点,但黑色节点是可以连续的。
因此若给定黑色节点的个数 N,最短路径的情况是连续的 N 个黑色,树的高度为 N - 1;最长路径的情况为节点红黑相间,树的高度为 2(N - 1) 。
性质 5 是成为红黑树最主要的条件,后序的插入、删除操作都是为了遵守这个规定。
红黑树并不是标准平衡二叉树,它以性质 5 作为一种平衡方法,使自己的性能得到了提升。
红黑树的左旋右旋

红黑树的左右旋是比较重要的操作,左右旋的目的是调整红黑节点结构,转移黑色节点位置,使其在进行插入、删除后仍能保持红黑树的 5 条性质。
比如 X 左旋(右图转成左图)的结果,是让在 Y 左子树的黑色节点跑到 X 右子树去。
我们以 Java 集合框架中的 TreeMap 中的代码来看下左右旋的具体操作方法:
指定节点 x 的左旋 (右图转成左图):
1 | //这里 p 代表 x |
可以看到,x 节点的左旋就是把 x 变成 右孩子 y 的左孩子,同时把 y 的左孩子送给 x 当右子树。
简单点记就是:左旋把右子树里的一个节点(上图 β)移动到了左子树。
指定节点 y 的右旋(左图转成右图):
1 | private void rotateRight(Entry p) { |
同理,y 节点的右旋就是把 y 变成 左孩子 x 的右孩子,同时把 x 的右孩子送给 x 当左子树。
简单点记就是:右旋把左子树里的一个节点(上图 β)移动到了右子树。
了解左旋、右旋的方法及意义后,就可以了解红黑树的主要操作:插入、删除。
总结
红黑树并不是真正的平衡二叉树,但在实际应用中,红黑树的统计性能要高于平衡二叉树,但极端性能略差。
红黑树的插入、删除调整逻辑比较复杂,但最终目的是满足红黑树的 5 个特性,尤其是 4 和 5。
在插入调整时为了简化操作我们直接把插入的节点涂成红色,这样只要保证插入节点的父节点不是红色就可以了。
而在删除后的调整中,针对删除黑色节点,所在子树缺少一个节点,需要进行弥补或者对别人造成一个黑色节点的伤害。具体调整方法取决于兄弟节点所在子树的情况。
红黑树的插入、删除在树形数据结构中算比较复杂的,理解起来比较难,但只要记住,红黑树有其特殊的平衡规则,而我们为了维持平衡,根据邻树的状况进行旋转或者涂色。
红黑树这么难理解,必定有其过人之处。它的有序、快速特性在很多场景下都有用到,比如 Java 集合框架的 TreeMap, TreeSet 等。